At the hacker event “End Summer Camp” 2024 I presented a joke talk about esoteric programming languages.

One of my favourite esolangs is Befunge and I wanted to create a themed quine with it. A quine is a program having an output that is equal to its source code.

This is my Befunge quine:

v@?/EndSummerCamp2024\     /Antani--Quine\           3s0l4ngu4g3s!
>88+20p"?@v",vhacking0   h0p3y0u3nj0yth1sr4       fcr34t1v1ty4nd1n
vo#d#o#o#,<#,<n1r4nd0m  cr4zy4t10n1mxfun4nd     y0uw4ntm0r3j0st4sk
>10g>1-:#v_$88*3+10p20  g1->20p     #E#S#C#    #y>#0>94+,#c#a#t#s>
  0x^1337       6o6o6o  l00k1ng               18>0#A^       4nt4n1
  H3ll0h0               h4ck1ng              l4ngu4N              
  99#love>88*2+\-20      g:#v_@3i7           23>88vT              
  y0ur3l00k1ngf0rs0       14>1-87+\-g,1      0g>#2vA              
  k0#s4n3xpr3ss10n0         3n1gmat1c1337    X08e0#N              
  m3r4nd0mt3xty0uv3            h3ll0h0w4r3   oX4av3I              
  42#miao                           xgh05t5  k0*c310              
  wh4ty0u       f0rg3t              cr4zy0v   <,#<-xb       xn1nj4
d0n3#1337#m4dn3ss@fun-  w1tch35     xn1ght>    p>1:n1-ht0x&h4ppy42
>#i>^wh1sperc4lls0fth3  d34d1nth3sh4d0w5th3     fl>1>0#d>p>#b#o#o>
4lw4y5h4v1ngth31r3y35o  gh05t5wh1sp3r4ndf1        4lway5s4tth3m3rg
f0rth3p0w3r5ofth3n1ght   d0ntf0rg3t1ts4l             l4b0uth4v1nfu

I tested it with an online Befunge-93 Interpreter.

In this post I want to add some details about how I created it.

The following image shows the effective execution path of the code (the orange characters):

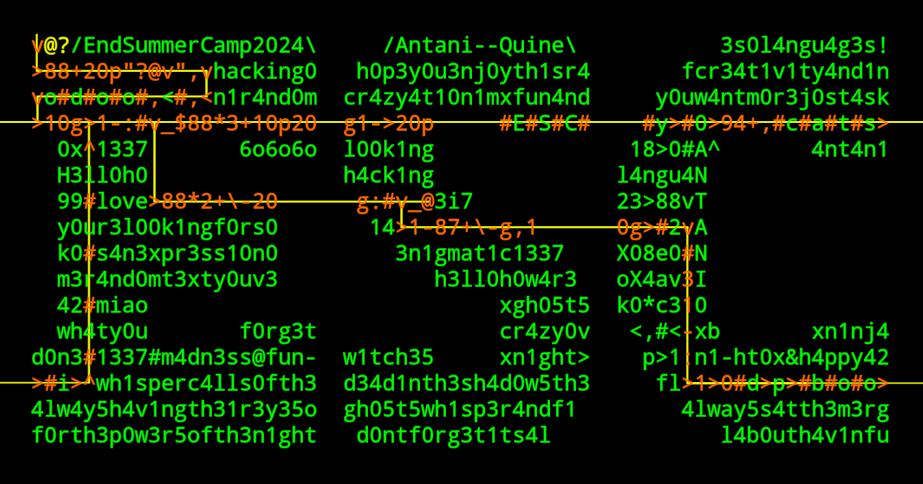
Befunge Quine with execution path

You can notice that most of the grid is filled with text that is not executable code but simple ASCII art that is read and then printed in the output. The base ASCII art has been generated with figlet and then I modified the content to fit the Befunge code and some custom text.

The second and third cells are marked in yellow because they are a bit special. They are used as data cells, to temporarily store the (x,y) coordinates of the cell that is going to be printed at each step of the loop (there is a loop for the rows and a loop for the columns). This is done with the special Befunge instructions g (get) and p (put), that allow you to read and write characters directly into the grid (by default data is stored into the stack). Since these 2 cells change their content we can’t read them, so it is necessary to print their values using the stack, before starting to read the other cells. This means that the code starts reading the grid at (3,0), after printing “v@?”.

The loops compute the coordinates to read decrementing two counters. The cell (1,0) has been initialized with the character @ because its ASCII value (64) corresponds to the width of the grid (67) minus 3 (the number of “special” cells). The height of the grid is smaller (16) and so a simple sum into the stack is used for initialization.

You can write Befunge code writing directly into the 2D grid, but without a proper planning it tends to become quite messy. So I drafted it thinking in a linear way, using a pseudocode where I marked some execution points with labels, in order to express goto and conditional instructions. It also gives me the possibility to add some comments, something that it is not possible to put in the quine.

I’ll use the following convention:

88+                    # [16]: the height
20p                    # put 16 (y) into (2,0)

"?@v",,,               # print the first 3 cells

[label0]               # retrieve x from (1,0)
10g                    # [x] (initialized to 64: the @ symbol)

[label1]
1-:                    # [x-1, x-1]
if stack.pop() == 0:   # [x-1]
  goto label2          # 
else:
  goto label4          # end of line reached

[label2]
88*2+                  # [x-1, 66]
\-                     # [66-(x-1)]: this is X
20g:                   # [X, y, y]
if stack.pop() == 0:   # [X, y]
  exit                 # reached last row (y == 0)
else:
  1-                   # [X, y-1]
  goto label3          # continue the loop in next column

[label3]
87+                    # [X, y-1, 15]
\-                     # [X, 15-(y-1)]: this is [X, Y]
g                      # retrieve the value from cell (X, Y)
,                      # print the value
10g1-:                 # [x-1, x-1]
10p                    # [x-1]; put x-1 into (1,0), so x = x-1
goto label1

[label4]               # end of line reached
$                      # discard x-1 (equals to 0) from stack
88*3+                  # [67]
10p                    # put 67 into (1,0)
20g1-                  # [y-1]
20p                    # put y-1 into (2,0), so y = y-1
94+,                   # print newline (13)
goto label0            # restart loop in next line

Then this logic has been rearranged into the grid adding Befunge 2D operators.